ОЛ ВЗМШ при МГУ: Отделение математики: Золотое сечение (А. Д. Бендукидзе)

ОЛ ВЗМШ при МГУ: Отделение математики


Избранные задачи Вопрос-Ответ

Авторы

Программы, темы

Поступающим

В помощь нашим ученикам

Отдохнуть

Если хочешь больше знать

Листовки к пособиям

Вход для наших учеников
Личный номер
Пароль

Золотое сечение (А. Д. Бендукидзе)

Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением.И если первое из этих сокровищ можно сравнить с мерой золота, то второе - с драгоценным камнем.

Теорему Пифагора знает каждый школьник, а что такое золотое сечение - далеко не все. Вот мы и решили рассказать читателям об этом драгоценном камне.

Что такое золотое сечение?

Говорят, что точка $C$ производит золотое сечение отрезка $AB$ , если

$AC:AB =CB:AC$ (1)

Итак, золотое сечение - это такое деление целого на две неравные части, при котором большая часть так относится к целому, как меньшая - к большей. В геометрии золотое сечение называется также делением оотрезка в крайнем и среднем отношении. Если длину отрезка $AB$ обозначить через $a$ , а длину отрезка $AC$ - через $x$ , то длина отрезка $CB$ будет $a-x$ , и пропорция (1) примет следующий вид:

$x:a = (a-x):x$ (2)

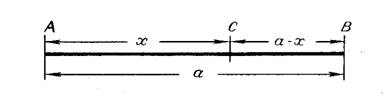
Из этой пропорции видно, что при золотом сечении длина большего отрезка есть среднее геометрическое, или, как часто говорят, среднее пропорциональное длин всего отрезка и его меньшей части: $x=\sqrt{a \cdot (a-x)}$

Легко сообразить, что верно и обратное: если отрезок разбит на два неравных отрезка так, что длина большего отрезка есть среднее геометрическое длин всего отрезка и его меньшей части, то мы имеем золотое сечение данного отрезка.

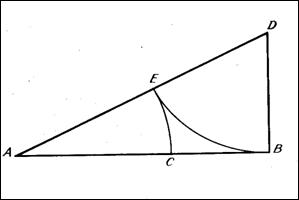Геометрически золотое сечение отрезка $AB$ можно построить следующим образом: в точке $B$ восставляем перпендикуляр к $AB$ и на нём откладываем $BD=0,5 \cdot AB$ ; далее, соединив точки $A$ и $D$ , откладываем $DE = BD$ и, наконец, $AC = AE$ . Точка $C$ является искомой - она производит золотое сечение отрезка $AB$ . В самом деле, заметим, что по теореме Пифагора $(AE+ED)^2=AB^2+BD^2$ ,

и по построению $AE=AC$ , $ED=BD=\frac{AB}{2}$ .

Из этих равенств следует, что

$AC^2+AC \cdot AB = AB^2$ ,

а отсюда уже легко получается равенство (1). Решая уравнение (2) относительно $x$ , мы находим, что

$x=\frac{-1+ \sqrt{5}}{2} \approx 0.62a$ .

Значит, $a-x \approx 0.35a$ . Таким образом, части золотого сечения составляют приблизительно 62% и 38% всего отрезка.

Немного истории

Древнейшим литературным памятником, в котором встречается деление отрезка в отношении золотого сечения, являются "Начала" Евклида ( III в. до н. э.). Уже во II книге ""Начал"" Евклид строит золотое сечение, а в дальнейшем применяет его для построения некоторый правильных многоугольников и многогранников.

Но золотое сечение было известно и до Евклида. В частности, знали о нем Пифагор и его ученики (VI век до н. э.). В философской Пифагора помимо философии и математики изучали и гармонию. Занимаясь теорией гармонии, пифагорейцы пришли к заключению, что качественные отличия звуков обусловлены количественными различиями между длинами струн. Это вдохновило их, и они постарались пойти дальше - выразить все закономерности мира через числа, полагая, что в основу мирового порядка бог положил именно число. Поэтому пифагорейцы в числах и их отношениях (а последние рассматривались как отношения отрезков) искали магическое, сверхъестественное. И в геометрии не обошлось без мистики. Здесь особо следует отметить любовь пифагорейцев к звёздчатому пятиугольнику, составленному из диагоналей правильного пятиугольника. Вот что пишет об этом известный математик и историк математики ван дер Варден в своей превосходной книге "Пробуждающаяся наука": "Эта фигура, символ здоровья, служила опознавательным знаком для пифагорейцев. Когда на чужбине один из них лежал на смертном одре и не мог заплатить человеку, который ухаживал за ним вплоть до его кончины, то он велел ему изобразить на своём жилище звёздчатый многоугольник; если когда-нибудь мимо пройдёт пифагореец, то он не преминет осведомиться об этом. Действительно, несколько лет спустя один пифагореец увидел этот знак, и хозяин дома получил богатое вознаграждение".

Звёздчатый пятиугольник для нас интересен в первую очередь тем, что каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения. В самом деле, так как треугольники $ACD$ и $ABE$ подобны, то $AC:AB = AD:AE$ . Но $AD=BC$ , а $AE=AC$ , и поэтому $AC:AB=BC:AC$ - уже известная нам пропорция золотого сечения. Именно это свойство звёздчатого пятиугольника и могли использовать пифагорейцы для построения правильного пятиугольника, ибо строить золотое сечение они, безусловно, умели.

К началу эпохи Возрождения усилился интерес к золотому сечению. Он был вызван, в первую очередь, многочисленными применениями золотого сечения как в самой геометрии, так и в искусстве, особенно в архитектуре. Следствием этого явилось появление книги "Божественная пропорция", автором которой был крупнейший математик XV века итальянец Лука Пачоли. В своем труде Пачоли приводит тринадцать свойств золотого сечения, которое он снабжает такими эпитетами, как "исключительное", "несказанное", "превосходнейшее", "замечательнейшее", "сверхъестественное" и так далее. Впрочем, название книги само говорит об отношении автора к описываемому предмету. Небезынтересно, что иллюстрировал книгу один из инициаторов её написания, друг Пачоли, великий Леонардо да Винчи. Между прочим, именно он ввёл сам термин "золотое сечение".

Лука Пачоли (около 1445 - позже 1509) - итальянский математик, написавший трактат о золотом сечении "Божественная пропорция".

Портрет Монны Лизы (Джоконды) был написан Леонардо да Винчи (1452- 1519) гениальным итальянским художником и ученым эпохи Возрождения. Картина привлекла внимание исследователей, которые обнаружили, что композиция рисунка основана на "золотых треугольниках" (точнее, на треугольниках, являющихся кусками правильного звёздчатого пятиугольника).

Наблюдения показывают, что с эстетической точки зрения золотое сечение имеет определённые достоинства. Это подтверждается экспериментом, который был проведен в конце прошлого века: из десяти прямо&угольников, среди которых был и "золотой" (со сторонами, отношение длин которых давало золотое сечение), испытуемый должен был выбрать один. И вот, около 22% общего числа испытуемых выбрало именно "золотой прямоугольник". Нельзя обойти молчанием и то, что книги, почтовые открытки, бумажники, шоколадные плитки и множество других предметов имеют форму золотого прямоугольника. Отметим здесь же, что если от "золотого" прямоугольника отрезать квадрат или к большей стороне "золотого" прямоугольника пристроить квадрат, то получится, снова "золотой" прямоугольник.

Широкое применение находит золотое сечение в архитектуре и искусстве. Множество архитектурных шедевров построено по пропорции золотого сечения. Эта же пропорция лежит в основе многих бессмертных творений Фидия, Тициана, Леонардо да Винчи, Рафаэля.

Греческий скульптор Леохар (4.в. до н. э.) создал статую Аполлона Бельведерского, воплотившего представления древних греков о мужской красоте. Линии, проведенные на снимке, определяют основные пропорции тела. Эти пропорции связаны с золотым сечением.

Отдали дань золотому сечению также композиторы и поэты. Известно, например, что на золотом сечении строил многие свои произведения выдающийся венгерский композитор Бела Барток. Что же касается поэтов, то здесь в первую очередь следует назвать гениального грузинского поэта Шота Руставели. Как показали новейшие исследования академика Г. В. Церетели, в основе строения поэмы Ш. Руставели "Витязь в тигровой шкуре" положены симметрия и золотое сечение. В частности, из 1587 строф поэмы больше половины - 863 - построены по пропорции золотого сечения...

Отношение золотого сечения и его замечательные свойства

Если в пропорции (2) положить $x=a \tau$ , то относительно $\tau$ получится следующее уравнение:

$\tau ^2+ \tau -1 = 0$ (3)

Положительный корень этого уравнения равен отношению золотого сечения: $\tau = \frac{x}{a} = \frac{a-x}{x}$

Это поистине замечательное число, обладающее рядом интересных свойств. Вот некоторые из них.

1. Непосредственные вычисления показывают, что $\tau = 0.618033989...$ , $\frac{1}{ \tau } = 1.618033989...$ - число, обратное $\tau$ , на единицу больше самого $\tau$ . Легко проверить, что это - единственное положительное число, обладающее таким свойством. В самом деле, если положительное $z$ удовлетворяет соотношению $\frac{1}{z}=1+z$ то $z$ должно быть корнем уравнения $z^2+z-1=0$ . Но это уравнение имеет единственный положительный корень: $z=\tau$ .

2. Переписав равенство (3) в виде $\tau = \frac{1}{1+\tau }$ и подставив в правую часть этого равенства $\frac{1}{1+ \tau }$ вместо $\tau$ , получим: $\tau = \frac{1}{1+\frac{1}{ \tau }}$

Этот процесс подстановки можно продолжить. В результате мы получим следующее представление числа $\tau$ в виде бесконечной цепной дроби:

$\tau = \frac{1}{1+\frac{1}{1+\frac{1}{1+\tau }}}$ (4)

Нельзя не отметить предельную простоту этого представления!

3. Вот ещё одно представление числа $\tau$ :

$\tau=\frac{1}{\sqrt{1+sqrt{1+\sqrt{1+...}}}}$ (5)

Чтобы придать смысл равенству (5), изучим последовательность

$sqrt{1}$ , $\sqrt{1+\sqrt{1}}$ , $\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1}}}}$ ,... ,

общий член которой (обозначим его через $\varphi_n$ ) содержит $n$ радикалов.

Непосредственно видно, что $\{\varphi_n\}$ - возрастающая последовательность. Кроме того, она ограничена. В самом деле, так как $\varphi_1 =1 <$ и $\varphi_{n+1}^2=\varphi_n+1$ , то из $\varphi_n< 2$ следует, что $\varphi_{n+1} <2$ , и по индукции заключаем, что $\varphi_n < 2$ для любого (натурального) $n$ .

Итак, $\{\varphi_n \}$ - возрастающая, ограниченная последовательность. А как известно, такая последовательность является сходящейся. Обозначив предел последовательности $\{\varphi_n\}$ через $\varphi$ , можно написать: $\varphi=\sqrt{1+\sqrt{1+\sqrt{1+...}}}=\lim_{n \to \infty}\varphi_n$ .

С другой стороны, переходя к пределу в равенстве $\varphi_{n+1}^2=1+\varphi _n$ , получим: $\varphi=\sqrt{1+\varphi}$ .

Таким образом, (положительное) число $\varphi$ является корнем квадратного уравнения $\varphi ^2-\varphi -1 =0$ , а $\psi = \frac{1}{\varphi }$ - корнем уравнения

$(1/ \psi)^2-\frac{1}{\psi}-1$ , или, умножая на $-\psi^2$ , $\psi^2-\psi-1$ , откуда $\psi = \tau$ ; $\varphi = \frac{1}{ \tau }$ - получаем равенство (5). И здесь бросается в глаза предельная простота представления!

Приближение числа $\tau$ рациональными числами

Представление (4) очень удобно для приближения иррационального числа $\tau$ рациональными числами. С этой целью обратимся к "подходящим" дробям:

$\tau _1=\frac {1}{1}$ , $\tau_2=\frac{1}{1+\frac{1}{1}}$ , $\tau_3=\frac{1}{1+\frac{1}{1+\frac{1}{1}}}$ , и вообще для любого $n$

$\tau_n=\frac{1}{1+\frac{1}{1+\frac{1}{1+...+\frac{1}{1}}}}$ . (6)

Последовательность этих дробей имеет пределом число $\tau$ , и поэтому каждое $\tau_n$ является приближением этого числа. Непосредственные вычисления показывают, что $\tau _1=\frac {1}{1}$ , $\tau _2=\frac {1}{2}$ , $\tau _3=\frac {2}{3}$ , $\tau _4=\frac {3}{5}$ , ...

Этот ряд дробей построен по очень простому закону: числитель каждой дроби равен знаменателю предыдущей дроби, а знаменатель - сумме числителя и знаменателя той же дроби. А как будет дальше? Сохраняется ли эта закономерность? Легко доказать, что это так. В самом деле, как видно из (6), соседние подходящие дроби $\tau_n$ и $\tau _{ n }$ связаны соотношением

$\tau _{ n +1}=\frac {1}{1+ \tau_n }$

и поэтому из равенства $\tau_n =\frac { m }{ k }$ следует, что $\tau_n =\frac { k }{ k + m }$

Этот простой закон образования подходящих дробей числа даёт возможность легко выписать их последовательность:

$\frac {1}{1}$ , $\frac {1}{2}$ , $\frac {2}{3}$ , $\frac {5}{8}$ , $\frac {8}{13}$ , $\frac {13}{21}$ ,...

Из теории цепных дробей известно, что подходящие дроби с нечётными номерами убывают и приближаются к порождающему эти дроби числу справа, а дроби с чётными номерами возрастают и приближаются к тому же числу слева. Применяя это свойство в нашем случае, можно написать:

$\frac {1}{2}<..< \tau < \frac {13}{21}< \frac {2}{3}$

Связь с числами Фибоначчи

Последовательностью Фибоначчи называется последовательность, первые два члена которой равны 1, а каждый последующий - сумме двух предыдущих. Таким образом, эта последовательность(обозначим ее через $\{ u_n \}$ ) определяется следующим образом:

$u _1=1$ , $u _2=1$ , $u _{ n +2}= u _{ n +1}+ u _{ n }$ ; ( $n = 1,2,3, ...$ ).

Вот первые члены этой последовательности: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,...

Вспомнив о приближениях числа $\tau$ подходящими дробями, мы заметим, что отношение любого члена последовательности Фибоначчи к последующему члену является подходящей дробюю числа $\tau$ , то есть приближенным значением отношения золотого сечения. Это приближение тем лучше, чем больше номер взятого члена.

Если же взять три последовательных члена: $u_n$ , $u _{ n +1}$ , $u _{ n +2}$ , то числа $\frac { u_n }{ u _{ n +1}}$ и $\frac { u _{ n +1}}{ u _{ n +1}}$ являются соседними подходящими дробями числа $\tau$ , причём одна из этих дробей больше $\tau$ , а другая меньше.

Наконец, поставим следующий вопрос: как разделить целое число $a$ на две целые части так, чтобы их отношение равнялось $\tau$ ?

Так как $\tau$ - иррациональное число, то такое деление, конечно, невозможно, интересующее нас отношение может лишь приближённо равняться $\tau$ . Каково же это приближение? Ответ на этот вопрос даёт теория цепных дробей.

Пусть знаменатель подходящей дроби $\tau_n$ есть $a$ . Рассмотрим множество всех дробей со знаменателями, не большими $a$ . Оказывается, из множества этих дробей ближе всех к числу $\tau$ находится именно $\tau_n$ .

Но знаменатели подходящих дробей являются членами последовательности Фибоначчи, поэтому если $a$ - член последовательности Фибоначчи, то деление $a$ с помощью $\tau_n$ будет хорошим приближением золотого сечения.

Таким образом, разделить золотым сечением на две целые части с хорошим приближением можно числа, являющиеся членами последовательности Фибоначчи. Например, золотое сечение числа 8 дает (3,5), числа 13 - (5,8) и т. д.