ОЛ ВЗМШ при МГУ: Отделение математики |
||

|
 |
|
| Избранные задачи Вопрос-Ответ | ||
К заданию первого курса
Подсказки к заданию 3.
Задача754. В киоске продаются 5 видов конвертов и 4 вида марок. Сколькими способами можно купить конверт и марку?
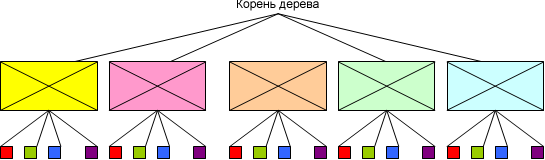
Подсказка. Рассмотрите таблицу и объясните, как она связана с этой задачей.
| м1 | м2 | м3 | м4 | |
| к1 | ||||
| к2 | ||||
| к3 | ||||
| к4 | ||||
| к5 |
А теперь рассмотрите дерево и объясните, как оно связано с задачей.
Задача 758. Сколькими способами можно поставить на шахматную доску белую и чёрную ладьи так, чтобы они не били друг друга?
Подсказка. Задача похожа на задачу755, решённую в книге. Ладья бьёт те фигуры, которые стоят с ней на одной горизонтали или на одной вертикали. Поэтому после того, как поставлена белая ладья, сколько остаётся мест для чёрной, на которых она не окажется под ударом белой?
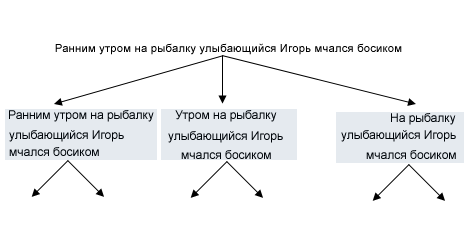
Задача 760.Можно рассуждать так: слово "ранним" можно включить в предложение, а можно не включать. Но если уж включить, то только вместе со словом "утром". А вот слово "утром" можно взять и без слова "ранним". Значит, для этих трёх слов есть 3 варианта вычёркивания:
вычеркнуть оба; оставить только "утром"; оставить "ранним утром".
"На рыбалку" можно вычеркнуть или оставить независимо от того, что вычеркнуто слева от него. Значит, сколько вариантов возможно для "Ранним утром на рыбалку"?
Продолжайте самостоятельно. Проверьте свой ответ с помощью дерева.
Задача 762. В нашем распоряжении есть три разных флага. На флагштоке поднимается сигнал, состоящий не менее, чем из двух флагов. Сколько различных сигналов можно поднять на флагштоке, если порядок флагов учитывается?
Подсказка. Так как флагов всего 3, не менее двух здесь значит два или три. Попробуйте нарисовать два дерева, одно для случая сигналов из двух флагов и одно для трёх.
Задача 763. Сколько разных чисел можно получить, переставляя цифры чисел:
а) 133; б) 9854; в) 3213; г)98 561; д)32 123.
Подсказка. В б) и в г) удобно рассуждать так: Рассмотрим полоску, в которой столько клеток, сколько цифр в числе:

Нам нужно заполнить её данными цифрами. Сколько есть вариантов заполнения первой слева клетки?
Сколько есть вариантов заполнения второй слева клетки после того, как первая уже заполнена? Во сколько раз число способов заполнения двух клеток больше числа способов заполнения одной клетки?
Сколько есть вариантов заполнения третьей слева клетки после того, как первые две уже заполнены? Во сколько раз число способов заполнения трёх клеток больше числа способов заполнения двух клеток?
Продолжайте самостоятельно.
В а), в) и д) такое рассуждение не проходит. Ведь если, например, в а) в первую слева клетку поставить 1, то для второй клетки останется только один вариант - 3. Если же в первую слева клетку поставить 3, то для второй клетки останется два варианта. Поэтому задача не решается просто умножением. И чем длиннее число, тем больше будет получаться разных случаев.
Можно рассуждать так. Сначала разместим обе цифры 3. В д), например, это можно сделать так:

После того, как размещены тройки, размещаем двойки. Сколько есть для этого вариантов? Во сколько раз число расстановок троек и двоек больше числа расстановок только троек?
Чёрная задача 763 решается точно так же.
Задача, похожая на 767. Вычислить: а)50!:47!; б) n!:(n-3)! .
Решение.
а)
;
;
.
б)
Задача 769.При приготовлении пиццы к сыру добавляются разные компоненты, обеспечивающие тот или иной вкус. В распоряжении Билла имеются перец, лук, грибы, помидоры, морковь и анчоусы, причём всё это можно, по его мнению, добавлять к сыру. Сколько типов пиццы может изготовить Билл?
Подсказка. Задача похожа на 760. Она даже проще, чем 760, тем, что все компоненты ведут себя так, как в 760 "на рыбалку" - их можно либо добавить в пиццу, либо не добавлять независимо от остальных компонент.
Задача 770. Грани куба можно окрасить либо все в белый цвет, либо все в чёрный, либо некоторые в белый, а некоторые в чёрный. Сколько существует разных способов окраски? (Два куба считаем окрашенными различно, если их нельзя перепутать, как ни вращай.)
Подсказка. Чем могут отличаться друг от друга разные способы? Прежде всего - числом чёрных граней. Поэтому имеет смысл рассмотреть отдельно случаи, когда чёрных граней 0, 1, 2, 3, 4, 5, 6.
Рассмотрим случай трех чёрных граней. Остальные случаи рассмотрите самостоятельно.
Все ли такие кубики одинаковы с точностью до поворотов? Нет.
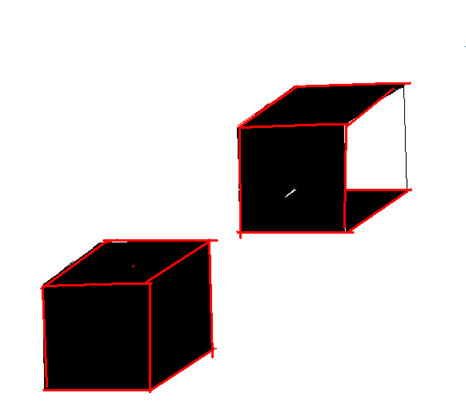
У верхнего куба есть две параллельные чёрные грани, а у нижнего их нет.
Подумайте, есть ли ещё какие-нибудь другие способы раскраски. Есть ли куб с тремя чёрными и тремя белыми гранями, который нельзя перепутать ни с одним из двух рассмотренных?
Задача 772. Сколько имеется трехзначных чисел, в запись которых входит ровно одна цифра 5?
Подсказка. Задача похожа на 763. Начните с размещения в
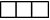
цифры 5.
Задача 774. Подсказка. Используйте подсказку в книге к 773.
Задача 775. На окружности даны 1987 точек, одна из которых выделена. Рассмотрите всевозможные выпуклые многоугольники с вершинами в этих точках. Каких многоугольников больше: тех, которые содержат выделенную точку, или тех, которые её не содержат?
Сначала решим задачу попроще, заменив в условии 1987 на 5.
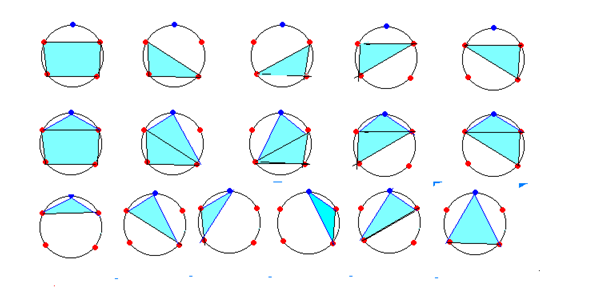
На рисунке в верхней строке изображены все варианты, для которых выделенная (синяя) точка не является вершиной.
![]() В средней строке под каждым из многоугольников из верхней строки нарисован тот, который получается при добавлении к множеству вершин синей вершины. Есть ли в средней строке повторяющиеся варианты? Почему? Все ли варианты с синей вершиной
В средней строке под каждым из многоугольников из верхней строки нарисован тот, который получается при добавлении к множеству вершин синей вершины. Есть ли в средней строке повторяющиеся варианты? Почему? Все ли варианты с синей вершиной
изображены в средней строке?
Какие варианты размещены в третьей строке?
Можно, конечно, подсчитать, сколько всего есть вариантов с синей вершиной, сколько без неё, и сравнить полученные числа. Но можно и не считать. Как вас учили в первом классе, чтобы сравнить число элементов в двух множествах, достаточно установить соответствие, при котором каждому элементу первого множества соответствует элемент другого, причём разным элементам первого множества соответствуют разные элементы второго. Тогда если во втором множестве остались лишние элементы, это значит, что во втором их больше. Как здесь установить такое соответствие?
Вернёмся к 1987 вершинам. Рисовать их, конечно, не стоит.
Заметьте, что какие бы три или больше из данных точек мы ни взяли, существует ровно один выпуклый многоугольник с вершинами в этих точках.
Теперь рассмотрим многоугольники, для которых выделенная точка вершиной не является. Мы всегда можем добавить к множеству вершин такого многоугольника и получить многоугольник, для которого выделенная точка - одна из его вершин. При этом если исходные многоугольники были разные, то есть отличались хоть одной вершиной, то и полученные из них многоугольники будут разными. Следует ли отсюда, что многоугольников с выделенной вершиной столько же, сколько без выделенной вершины? Почему? Какой отсюда вывод?
Подсказки к дополнительным задачам.
Задача 771. Шириной прямоугольника назовём длину наименьшей из его сторон. (Ширина квадрата - длина любой из его сторон.) Сколькими способами можно вырезать из шахматной доски прямоугольник шириной3? (Разрезы должны идти только по границам клеток.)
Подсказка. Можно рассуждать так. Сначала найдите, сколькими способами можно вырезать прямоугольник со сторонами 3 и 8.
После этого найдите, сколькими способами из такого прямоугольника можно вырезать прямоугольник ширины 3 . (Считайте, что сам прямоугольник со сторонами 3 и 8 можно вырезать из себя).
Умножьте число способов вырезать прямоугольник ширины 3 из прямоугольника со сторонами 3 и 8 на число прямоугольников со сторонами 3 и 8. Получится ли при этом ответ на вопрос задачи? Какие прямоугольники будут подсчитаны дважды? Сколько прямоугольников подсчитано дважды? Осталось вычесть это число из произведения.
Задача 777. Натуральное число делится на 12 и имеет 14 различных делителей. Найдите это число.
Подсказка. Сначала прочтите текст на голубом фоне на стр.120 книги и решите задачу 776. После этого решите уравнение
,
где и
,
,...,
- неизвестные натуральные числа.
Может ли быть 3 или больше трёх? Почему? Чему равно
? Может ли быть
и
?
Задачи 778 и 779 похожи на 777.
