ОЛ ВЗМШ при МГУ: Отделение математики: Разбор задач

ОЛ ВЗМШ при МГУ: Отделение математики


Избранные задачи Вопрос-Ответ

Авторы

Программы, темы

Поступающим

В помощь нашим ученикам

Отдохнуть

Если хочешь больше знать

Листовки к пособиям

Вход для наших учеников
Личный номер
Пароль

Разбор задач

1(6-10).Найдите правильную дробь, которая увеличится в 3 раза, если её числитель возвести в куб и одновременно к знаменателю прибавить число 3.

Решение. Пусть x - числитель ,a y - знаменатель дроби, x и у - натуральные числа .

	Числитель	Знаменатель	Вся дробь
было	$x$	$y$	$\frac{x}{y}$
стало	$x^3$	$y+3$	$\frac{x^3}{y+3}$ УВЕЛИЧИЛАСЬ В 3 РАЗА

На основании связи между числами в третьем столбце составляем уравнение: $3x/y=x^3/(y+3)$ или $3x(y+3)=x^3y$ или (так как $x$ - натуральное число) $3(y+3)=x^2y$ ; $x^2y-3y=9$ ; $y(x^2-3)=9$ .

Так как $x$ и $y$ - натуральные числа, $y=1$ , $x^2-3=9$ , или $y=3$ , $x^2-3=3$ , или $$y=9$ , $x^2-3=1$ . Годится только последний вариант: $y=9$ , $x=2$ .

Ответ: $2/9$

2(7-10). Могут ли две биссектрисы треугольника быть взаимно перпендикулярными?

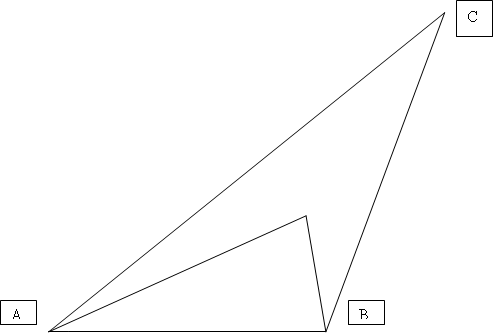Решение Пусть $ABC$ - произвольный треугольник, $\angle A = \alpha$ , $\angle B= \beta$ , $\angle C = \gamma$ . Тогда $\alpha +\beta + \gamma =180^o$ , $\alpha +\beta =180^o - \gamma$ .

Теперь рассмотрим треугольник $ABO$ , где $O$ - точка пересечения биссектрис треугольника $ABC$ . В нем $\angle OAB=\alpha /2$ , $\angle OBA = \beta /2$ . Значит $\angle ABO=180^o-\alpha /2- \beta /2=90^o+90^o- \alpha /2- \beta /2=90^o +(180^o - \alpha - \beta )/2=90^o+ \gamma /2>90^o$ .

Ответ. Не могут.

3(8 - 10). Первая,вторая и третья цистерны одинакового объёма начинают одновременно наполняться нефтью со скоростями 100, 60 и 80 литров в минуту соответственно. Сначала первая цистерна пуста, а вторая и третья частично заполнены. Известно, что все три цистерны будут заполнены полностью одновременно. Во сколько раз первоначальное количество нефти во второй цистерне больше, чем в третьей?

Решение.

	Первоначальное количество в л.	Скорость работы в л/мин	Время в мин.	Объем нефти в цистерне в л.
1-ая цистерна	0	100	одинаковое	одинаковое
2-ая цистерна	$x$	60
3-я цистерна	$y$	80

Требуется найти $x/y$ .

Обозначим время работы через $t$ . Заполним таблицу.

	Первоначальное количество в л.	Скорость работы в л/мин	Время работы в мин.	Объём нефти в л. к концу работы
1-ая цистерна	0	100	$t$	оди- $100t$
2-ая цистерна	$x$	60	$t$	нако- $x + 60t$
3-я цистерна	$y$	80	$t$	вое $y+ 80t$

На основании равенства всех чисел в последнем столбце получаем два уравнения: $100t=60t+x$ и $100t=80t+y$ .

Неизвестных больше,чем уравнений. Поэтому однозначно найти значения всех неизвестных не удастся. Но нас интересует только $x/y$ . Выразим $x$ и $y$ через $t$ .

$x= 40t$ и $y=20t$ . Значит $x/y =2$ .

Ответ. В 2 раза.

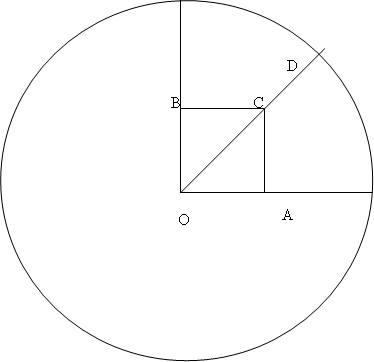4(8-10). Найдите радиус окружности, вписанной в четверть единичного круга (окружность должна касаться и дуги круга, и ограничивающих четверть круга радиусов).

Решение. Пусть $O$ - центр данной окружности, $C$ - искомой. Пусть $A$ , $B$ и $D$ - точки, в которых искомая окружность касается границ четверти исходного круга. Пусть радиус искомой окружности равен $x$ . Тогда $\angle CBO = \angle CAO=90^o$ , $CB =CA=x$ . Значит $ACBO$ - квадрат со стороной $x$ .

Точки $O$ , $C$ и $D$ лежат на одной прямой, и $OC=OD-CD=1-x$ . Так как в равнобедренном прямоугольном треугольнике квадрат гипотенузы равен удвоенному квадрату катета, получаем уравнение $2x^2=(1-x)^2$ .

Решим уравнение: $2x^2-(1-2x+x^2)=0$ ; $x^2+2x-1=0$ ; $x^2+2x+1=2$ ; $(x+1)^2=2$ .

Так как $x>0$ , то $x+1=\sqrt{2}$ ; $x =\sqrt{2} -1$ .

Ответ: $x =\sqrt{2} -1$ .

5(6-10). Простое или составное число $5^{14}-2^6 \cdot 5^7+2^{10}$ ? (Простым называется натуральное число, большее единицы, которое делится только само на себя и на единицу.)

Решение. Заметим, что $5^{14}-2^6 \cdot 5^7+2^{10}=5^{14}-2 \cdot 2^5 \cdot 5^7+2^{10}=a^2-2ab+b^2$ , где $a= 5^7$ , а $b=2^5$ .

Значит $5^{14}-2^6 \cdot 5^7+2^{10} =(5^7-2^5)^2=(5^7-2^5)(5^7-2^5)$ .

Итак, $5^{14}-2^6 \cdot 5^7+2^{10}$ делится на $5^7-2^5$ . При этом $5^7-2^5=5^3 5^4-32>125-32>1$ .

Ответ: составное.

6(7-10). Найдите углы треугольника, если две его стороны видны из центра описанного около него круга под углами 20°и 30° соответственно.

Решение. Будем использовать сведения из курса геометрии за восьмой класс: центральный угол измеряется дугой, на которую он опирается, а вписанный - половиной дуги. Отсюда следует, что одна сторона нашего треугольника разбивает окружность на дуги в 20° и 360°-20°=340°, а другая - на дуги в 30° и 330°. Значит лежащие против этих сторон углы равны соответственно один 10° или 170°, а другой - 15° или 165°. Так как у треугольника не может быть больше одного тупого угла, то остаются варианты 10°; 165°, или 15°; 170°, или 10°; 15°. При этом вариант 15°; 170° отпадает потому, что сумма углов треугольника всегда равна 180°, а 15°+170°>180°. Остались варианты 10°; 165°; 5° и 10°; 15°; 155°. Оба варианта удовлетворяют условию задачи.

Ответ: 10°; 165°; 5° или 10°; 15°; 155°.

7(6-10). Найдите трехзначное число, если известно, что три последних цифры его квадрата образуют само это число.

Решение. Пусть $A$ - искомое число. Тогда последние три цифры числа $A^2-A$ равны 0. Значит $A^2-A$ делится без остатка на $1000=2^35^3$ . Но $A^2-A=A(A-1)$ , где числа $A$ и $A-1$ - соседние в натуральном ряду. Значит в разложение одного из этих чисел на простые множители должно входить три двойки, а в разложение другого - три пятёрки. Значит либо $A$ , либо $A-1$ равно одному из чисел 125, 250, 375, 500, 625, 750, 875. Проверяем: 125 при делении на 8 даёт остаток 5, 250 - остаток 2, 375 - остаток 7, 500 - остаток 4, 625 - остаток 1, 750 - остаток 6, 875 - остаток 3. Подходят только варианты $A=376$ ; $A-1=375$ и $A=625$ ; $A-1=624$ .

Ответ: 376 или 625.

8(8 -10). Через точку $K$ , взятую внутри окружности, проведены хорды $AB$ и $CD$ , причём $AK=2, CK=7$ . Радиус окружности, вписанной в треугольник $ADK$ , равен 1. Каков радиус окружности, вписанной в треугольник $CBK$ ?

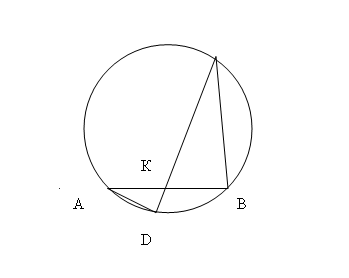Дано: $AB$ и $CD$ - хорды одной окружности, $K$ - их точка пересечения. $AK=2$ ; $CK=7$ . Радиус окружности, вписанной в треугольник $ADK$ равен 1. Найти радиус r окружности, вписанной в треугольник $CBK$

Решение. По чертежу правдоподобно, что треугольники $AKD$ и $CBK$ подобны. Выясним, обязательно ли они подобны или случайно оказались такими на чертеже.

$\angle AKD = \angle CKB$ , как вертикальные. $\angle DAB=\angle DCB$ , так как это вписанные углы, измеряющиеся половиной одной и той же дуги. Значит треугольники действительно подобны . А отношение радиусов вписанных окружностей равно коэффициенту подобия, то есть $r:1=CK:AK=7:2. Отсюда r=7:2=3,5$ .

Ответ: 3,5.

9(8-10). Решите систему уравнений, если $y$ и $z$ - простые числа ( см. условие задачи № 4).

$1/x+1/y=1/z, \\x= yz$ .

Решение. Заметим, что из $x=yz$ следует, что не только $y$ и $z$ , но и $x$ должно быть натуральным числом. Подставим в первое уравнение вместо х выражение yz. Получим $1/yz+1/y=1/z$ ; $(1+z)/yz=1/z$ .

Так как $y>0$ ; $z>0$ , то можно умножить обе части уравнения на yz. Получим $1+z = y$ .

Итак, $y$ и $z$ не просто два простых числа, а ещё и у только на 1 больше, чем $z$ .

Значит одно из этих чисел чётное. Так как, кроме 2, простых чётных чисел нет, то $z=2$ ; $y=3$ . Тогда $x= 2\cdot 3 = 6$ .

Ответ: (6; 3; 2).

10(8-10). На катете прямоугольного треугольника как на диаметре построена окружность. Оказалось, что она делит его гипотенузу в отношении 1:3. Найдите углы треугольника.

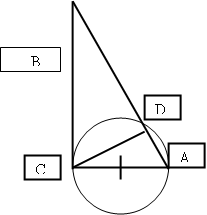Дано: $\angle C$ треугольника $ABC$ прямой; $O$ - центр окружности; $O$ лежит на $AC$ . $D$ - точка пересечения окружности и $AB$ . $AD:DB=1:3$ или $3:1$ . Найти $\angle CAB$ и $\angle CBA$ .

Решение. Так как $\angle CDA$ - вписанный угол, опирающийся на диаметр, то $\angle CDA = 90^o$ . Значит треугольники $CBD$ и $CDA$ прямоугольные, причём оба они подобны треугольнику $ABC$ , так как у каждого из них с треугольником $ABC$ есть общий острый угол. Так как высота из вершины $C$ у треугольников $CDA$ и $CBD$ общая, то отношение их площадей равно отношению $BD$ к $DA$ . Значит площадь одного из них составляет 1/4, а другого 3/4 площади треугольника $ABC$ . А так как площади подобных фигур относятся как квадраты их линейных размеров, то коэффициент подобия треугольников $ABC$ и $ADC$ равен $1/2$ или $\sqrt{3/2}$ . Так как $AC$ и $AB$ - гипотенузы этих треугольников, то $AC/AB$ равно $1/2$ или $\sqrt{3/2}$ . Значит угол $A$ равен $30^o$ или $60^o$ .

Ответ: $30^o$ или $60^o$ .

11(6-10). Решите уравнение, если $a$ , $b$ и $c$ - положительные числа.

$(a+b-x):c + (a+c-x):b + (b+c-x):a + 4x:(a+b+c) = 1$ .

Решение. Заметим, что $(a+b-x):c=(a+b+c-x-c):c= (a+b+c-x):c-1$ ; аналогично

$(a+c-x):b= (a+b+c-x):b-1; \\ (b+c-x):a=(a+b+c-x):a-1$ .

Обозначим $a+b+c-x$ через $y$ . Получаем x= $a+b+c-y^$ ; $x:(a+b+c)=(a+b+c-y):(a+b+c)=1-y:(a+b+c)$ ; $y/c - 1 + y/b - 1 + y/a - 1 + 4- 4y/(a+b+c)= 1$ ; $y(1/c+1/b+1/a-4/(a+b+c)) = 0$ .

Произведение равно нулю в том и только в том случае, если хотя бы один множитель равен нулю. Значит, если $1/c + 1/b + 1/a - 4/(a+b+c)$ не равно нулю, то $y=0$ , а $x=a+b+c$ .

Обозначим $1/c + 1/b + 1/a - 4/(a+b+c)$ через $P$ . Осталось выяснить, обращается ли $P$ при каких-нибудь $a$ , $b$ и $с$ в нуль. Имеем $P(a+b+c) = (a+b+c)/c + (a +b+c)/b + (a+b+c)/a - 4 =a/c + b/c + 1 + a/b + 1 + c/b + 1 + b/a + c/a - 4 =a/c + c/a + b/c + c/b + a/b +b/a - 1$ . Так как $a$ , $b$ и $с$ - положительные числа, то хотя бы одно из чисел $a/b$ и $b/a$ не меньше 1 и хотя бы одно из чисел $a/c$ и $c/a$ не меньше 1. Значит $P (a+b+c) \geq 1+1-1= 1$ и $P$ не обращается в нуль ни при каких значениях $a$ , $b$ , $c$ .

Ответ. При любых положительных значениях $a$ , $b$ , $c$ уравнение имеет ровно один корень: $x =a+b+c$ .

12(6-10). Имеется набор одинаковых правильных картонных треугольников, вершины которых как-то занумеровали цифрами 1,2,3 так, что в каждом треугольнике все вершины имеют разные номера. Затем треугольники аккуратно сложили в стопку, совместив их вершины, и подсчитали сумму номеров вершин в каждом углу стопки. Могут ли все три суммы равняться: а) 55; б) 50.

Решение. Заметим, что при сложении всех трёх сумм получится сумма номеров всех вершин всех этих треугольников. Её можно найти другим способом: сначала сложить номера всех вершин одного треугольника (получится 1+2+3=6), а потом умножить на количество треугольников. Значит полученная в результате сумма обязательно должна делиться на 6. Но 55. 3 на 6 не делится. Следовательно случай а) невозможен. В случае б) получаем (50. 3) : 6 = 25 - целое число. Значит ли это, что на вопрос б) можно уже дать положительный ответ? Пока нет. Ответ "могут'' считается обоснованным только если конкретно указан способ, как это можно сделать. Из того, что 150: 6= 25, следует только, что нужно попытаться взять 25 треугольников и расположить их так, чтобы сумма номеров в каждом углу стопки равнялась 50. Попробуем положить $x$ треугольников тройкой в первый угол стопки и единицей во второй, $y$ треугольников единицей в первый угол и тройкой во второй, $z$ треугольников двойкой в первый и тройкой во второй и остальные $25-x-y-z$ треугольников единицей в первый и двойкой во второй. получаем два уравнения:

$3x+y+2z+(25-x-y-z) = 50; \\ x+3y+3z+2(25-x-y-z)=50$ . После приведения подобных $2x+z= 25;\\-x+y+z=0$ .

Отсюда $x = y+z$ ; $2(y+z)+z = 25$ ; $2y+3z= 25$ . Уравнению $2y +3z=25$ удовлетворяет несколько пар неотрицательных целых чисел $(y;z)$ . Но нам не нужны все, а достаточно одной. Возьмём y=z=5. Тогда $x=10$ . Итак, мы нашли вариант расположения треугольников, при котором сумма номеров в двух углах, а значит и в третьем, равна 50.

Ответ. а) нет; б) да.

13(8-10). Упростите выражение $\frac{(x-b)(x-c)}{(a-b)(a-c)}+\frac{(x-c)(x-a)}{(b-c)(b-a)}+\frac{(x-a)(x-b)}{(c-a)(c-b)}$

Решение. Понятно, что достаточно рассмотреть случай, когда $a \neq b$ ; $b \neq c$ ; $a \neq c$ , так как иначе один из знаменателей обращается в нуль и выражение не имеет смысла.

$\frac{(x-b)(x-c)}{(a-b)(a-c)}+\frac{(x-c)(x-a)}{(b-c)(b-a)}+\frac{(x-a)(x-b)}{(c-a)(c-b)} = \\ \frac{(c-b)(x-b)(x-c)+(a-c)(x-c)(x-a)+(b-a)(x-a)(x-b)}{(a-b)(b-c)(c-a}$

Мы видим, что если раскрыть скобки и сгруппировать члены по степеням $x$ , то получится

многочлен вида $P(x)=Ax^2 + Bx + C$ , где $A$ , $B$ , $C$ не содержат $x$ , а сами представляют собой дроби, числители и знаменатель которых - многочлены с тремя переменными $a$ , $b$ , $c$ . Осталось найти $A$ , $B$ и $C$ . Подставим вместо $x$ $a$ . Получим

$P(a) = (c-b)(a-b)(a-c)+(a-c)(a-c)\times 0 + (b-a)\times 0 \times (a-b) = (c-b)(a-b)(a-c) = (a-b)(b-c)(c-a)$ .

Аналогично получим, что $P(b)$ и $P(c)$ тоже равны $(a-b)(b-c)(c-a)$ . Но многочлен второй или первой степени не может принимать одно и то же значение сразу в трёх точках. Значит $P(x)$ - многочлен нулевой степени, то есть $A$ и $B$ равны нулю при всех значениях $a$ , $b$ , $c$ , а $C$ при всех $a$ , $b$ , $c$ , равно $(a-b)(b-c)(c-a)$ . Если считать известным, что многочлен с несколькими переменными может быть равен нулю при всех значениях переменных, то получим, что числители дробей $A$ , $B$ и $C-(a-b)(b-c)(c-a)$ , а после приведения подобных обращаются в 0, $C$ обращается в $(a-b)(b-c)(c-a)$ , а всё исходное выражение в $\frac{(a-b)(b-c)(c-a)}{(a-b)(b-c)(c-a)} = 1$

Проверим это конструктивно:

$\frac{(x-b)(x-c)}{(a-b)(a-c)}+\frac{(x-c)(x-a)}{(b-c)(b-a)}+\frac{(x-a)(x-b)}{(c-a)(c-b)} = \\ \frac{(c-b)(x-b)(x-c)+(a-c)(x-c)(x-a)+(b-a)(x-a)(x-b)}{(a-b)(b-c)(c-a)}= \\ \frac{x^2(c-b)+ x(b+c)(c-b) +bc(c-b) + x2(a-c) -x(a+c)(a-c) + ac(a-c)+x^2(b-a)-x(a+b)(b-a)+ab(b-a) }{(a-b)(b-c)(c-a)} = \\ \frac{ x^2((c-b)+(a-c)+(b-a)) - x((c^2-b^2)+(a^2-c^2)+(b^2-c^2))+((bc^2-cb^2)+(ca^2-ac^2)+(ab^2-ba^2)) }{ (a-b)(b-c)(c-a) } = \\ \frac{ x^2 \times 0- x \times 0 +bc^2-ac^2+ca^2-cb^2+ab^2-ba^2 }{ (a-b)(b-c)(c-a) } = \\ \frac{ -c^2(a-b) +c(a+b)(a-b) -ab(a-b) }{ (a-b)(b-c)(c-a) } = \\ \frac{ (a-b)(-c^2+ac+bc-ab) }{ (a-b)(b-c)(c-a) } = \frac{ (a-b)(-c^2+ac+bc-ab ) }{ (a-b)(b-c)(c-a) }= \frac{ (a-b)(bc-c^2-ab+ac) }{ (a-b)(b-c)(c-a) } = \\ \frac{ (a-b)(c(b-c)-a(b-c)) }{ (a-b)(b-c)(c-a) }= \\ \frac{ (a-b)(b-c)(c-a) }{ (a-b)(b-c)(c-a) }$ .

При $a \neq b$ ; $b \neq c$ ; $a \neq c$ это выражение обращается в 1.